本帖最後由 22169751 於 2016-6-3 18:05 編輯
1.已知x,y均為整數,且滿足(\frac{1}{x^{2}}+\frac{1}{y^{2}})=-\frac{2}{3}(\frac{1}{x^{4}}-\frac{1}{y^{4}})) ,試求x+y之值有幾種可能。 ,試求x+y之值有幾種可能。
2.已知非負實數x,y,z滿足x+y+z=1,試求2xy+yz+2zx的最大值。
3.六張不同的卡片上分別有數字2、2、4、4、6、6,從中取出三張,試求這三張所寫的卡片可作為三角形三邊長的機率。
4.已知正整數a,b,c滿足1<a<b<c,a+b+c=111,b²=ac,試求b之值。
5.在銳角ΔABC中,已知√3tanAtanB-tanA-tanB=√3且c=2,試求a²+b²的範圍。
6.已知關於x的方程式x²-4xlog2 a+3(log2 a)²=0的兩根分別屬於區間(1,3)與(6,∞),試求實數a的取值範圍。
7.在ΔABC中,已知a=5,b=4,cos(A-B)= ,試求ΔABC的面積。 ,試求ΔABC的面積。
8.在ΔABC中,已知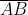 = =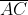 ,D為邊 ,D為邊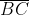 上的中點, 上的中點, ⊥ ⊥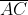 於點E, 於點E, 與 與 交於點P,若 交於點P,若 =3, =3, =1,試求 =1,試求 之值。 之值。
9.假設實數a,b滿足+b(b+2a)=40\\a(b+1)+b=8\end{cases}) ,試求 ,試求 之值。 之值。
10.試求所有的自然數n,使得 為一個自然數的平方。 為一個自然數的平方。
這份題目我寫了一個小時沒解出半題
有興趣的自己試試看吧
答案視作答情況公布
先公布答案型式(Ⓧ表示0,1,2,3,4,5,6,7,8,9,-,±其中一個,如-2√3會以ⓍⓍ√Ⓧ呈現)
被解出來的題目就以數字顯示
1.Ⓧ
2.
3.
4.36
5. <a²+b²≦Ⓧ <a²+b²≦Ⓧ
6.Ⓧ<a<Ⓧ
7.
8.√2
9.8
10.12 |